Mnemonic for Riemann Curvature Tensor

It’s been a year now, I rarely write blog posts. I hope you guys are still following my blog. In this short post, I’m very happy to share the mnemonic that I discovered.

Long story short, I don’t like the fact that I have to remember the indices place in Riemann Curvature Tensor. Please comment if you also felt the same. So, I take my time to find a mnemonic for this formula. Voilà: I found it.

Let me first remind you of the formula for Riemann Curvature Tensor,

$R^{\rho}_{\hspace{0.15cm}\sigma \mu \nu} = \partial_{\mu} \Gamma^{\rho}_{\nu \sigma} - \partial_{\nu} \Gamma^{\rho}_{\mu \sigma} + \Gamma^{\rho}_{\mu \lambda}\Gamma^{\lambda}_{\nu \sigma} - \Gamma^{\rho}_{\nu \lambda}\Gamma^{\lambda}_{\mu \sigma}$.

I’m naming partial derivative $\partial_{\square}$ as P and Christoffel connection $\Gamma^{\square}_{\square\square}$ as C. And, $\square$ means index to be filled. So, I write right-hand side part of Riemann Curvature Tensor as

$R^{\rho}_{\hspace{0.15cm}\sigma \mu \nu} = + \text{PC} - \text{PC} + \text{CC} - \text{CC}$.

Our mnemonic is actually this: you can spell the right-hand side as PC, PC, CC, CC and then insert $+$ and $-$ sign consecutively.

So, our initial form looks like this:

$R^{\rho}_{\hspace{0.15cm}\sigma \mu \nu} = + \hspace{0.2cm} \partial_{\square} \Gamma^{\square}_{\square\square} \hspace{0.2cm} - \hspace{0.2cm} \partial_{\square} \Gamma^{\square}_{\square\square} \hspace{0.2cm} + \hspace{0.2cm} \Gamma^{\square}_{\square\square} \Gamma^{\square}_{\square\square} \hspace{0.2cm} - \hspace{0.2cm} \Gamma^{\square}_{\square\square} \Gamma^{\square}_{\square\square}$.

Now, the only step remaining is to find a way to insert the indices in $\partial_{\square}$ and $\Gamma^{\square}_{\square\square}$. By looking just the formula, it’s quite easy to remember the place of $\rho$ and dummy index $\lambda$ which is at

$R^{\rho}_{\hspace{0.15cm}\sigma \mu \nu} = + \hspace{0.2cm} \partial_{\square} \Gamma^{\rho}_{\square\square} \hspace{0.2cm} - \hspace{0.2cm} \partial_{\square} \Gamma^{\rho}_{\square\square} \hspace{0.2cm} + \hspace{0.2cm} \Gamma^{\rho}_{\square\lambda} \Gamma^{\lambda}_{\square\square} \hspace{0.2cm} - \hspace{0.2cm} \Gamma^{\rho}_{\square\lambda} \Gamma^{\lambda}_{\square\square}$.

So, let’s make a visualization to find a way to insert $\sigma$, $\mu$ and $\nu$ indices. In $R^{\rho}_{\hspace{0.15cm}\sigma \mu \nu}$, let’s only observe the position of lower indices $\sigma \mu \nu$ as

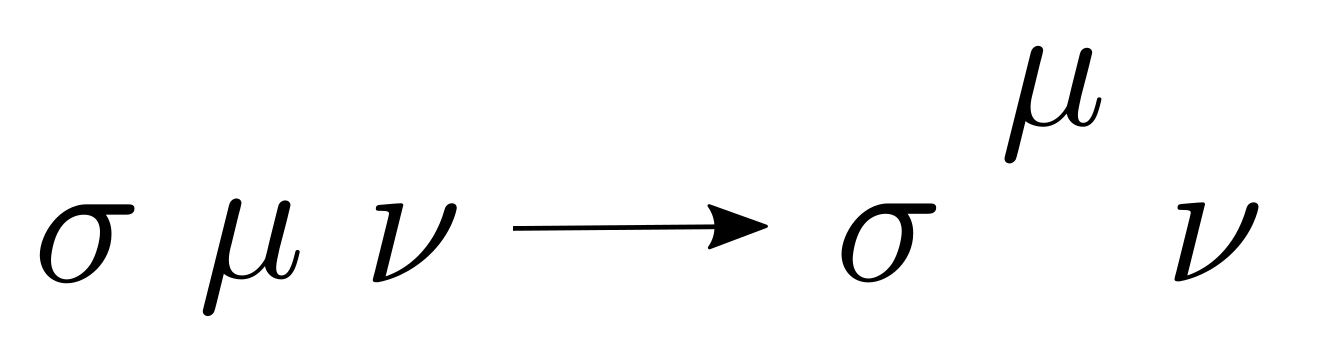
. For $+$ sign, the index goes clockwise direction starting from $\mu$ as

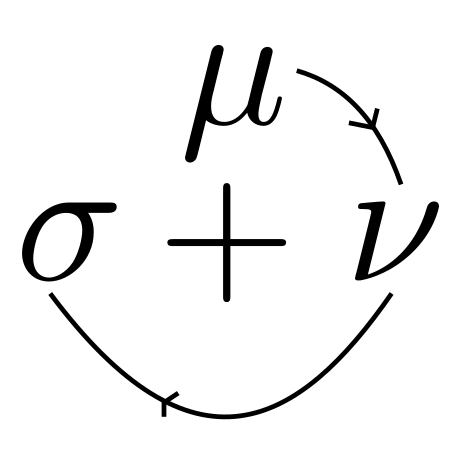
i.e. $\mu\nu\sigma$ and for $-$ sign, the index goes anti-clockwise direction starting from $\nu$ as

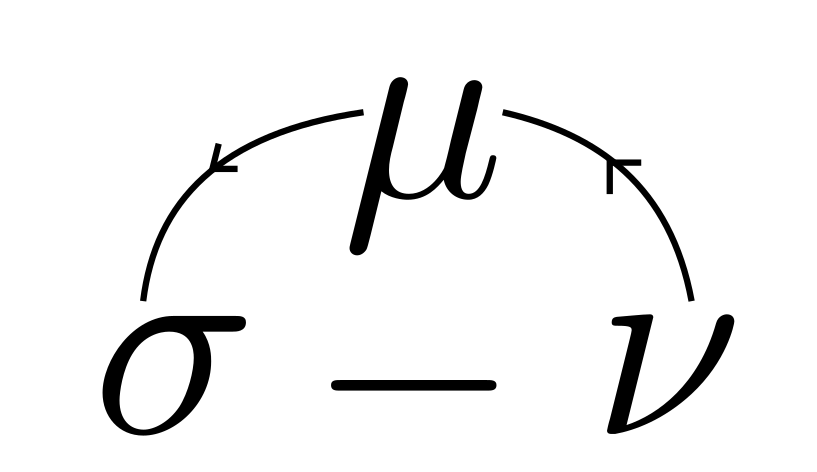
i.e. $\nu\mu\sigma$. Then replace three square boxes (I mean $\square)$ on each term of Riemann Curvature Tensor. Surprise! You will see this

$R^{\rho}_{\hspace{0.15cm}\sigma \mu \nu} = \partial_{\mu} \Gamma^{\rho}_{\nu \sigma} - \partial_{\nu} \Gamma^{\rho}_{\mu \sigma} + \Gamma^{\rho}_{\mu \lambda}\Gamma^{\lambda}_{\nu \sigma} - \Gamma^{\rho}_{\nu \lambda}\Gamma^{\lambda}_{\mu \sigma}$.