An introduction to F-notation

Many many years ago, human beings (We) invented counting. Since then the concept related to counting is probably the greatest discovery in the initial phase of mathematics. We know more about the number systems like real numbers $\mathbb{R}$, rational numbers $\mathbb{Q}$, natural numbers $\mathbb{N}$, and so on. And also, divided the number systems into two categories based on counting i.e. Countable sets and Uncountable sets. This concept advances “Set Theory” which was first proposed by George Cantor and followed by Richard Dedekind and many more.

In this post, I want to introduce a new type of notation which I named “F-notation”. You will know at last, why I need to introduce this, how the name came into my mind, and how it will help to prove one of the well-known theorems of Number theory.

So, the strategy goes like this: first, I will create the necessary ingredients for the given statement “The set $\mathbb{N}\times \mathbb{N}$ is countably infinite”. This means the cartesian product of natural numbers is countably infinite, and countably infinite means you can able to find or count a natural number even at infinity. In the middle of the procedure, I will introduce F-notation. Let’s get started!

Theorem. The set $\mathbb{N}\times \mathbb{N}$ is countably infinite.

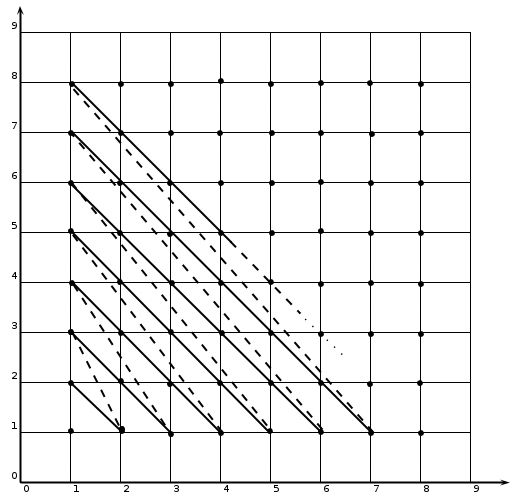
Proof. We know, $\mathbb{N}\times \mathbb{N} \to \mathbb{N}$. So the cartesian graph looks like the above figure. I want to introduce two definitions.

Definition 1. The ordered pair can be written as $a_{x}+b_{y}$ where a is the first entry which lies on $x$ coordinate and b is the second entry which lies on $y$ coordinate. And, $a_{x}+b_{y}$ will give the solution as $a+b$ (i.e. $a_{x}+b_{y}=a+b$) such that $a_{x}$ and $b_{y}$ are greater than zero, and also not equal to zero.

First, we will pick out the diagonal points (i.e. ordered pairs) from the above figure. From definition 1, we can write

$ 1_{x}+1_{y} = 2 $

$ 1_{x}+2_{y} = 2_{x}+1_{y} = 3 $

$ 1_{x}+3_{y} = 2_{x}+2_{y} = 3_{x}+1_{y} = 4 $

$ 1_{x}+4_{y} = 2_{x}+3_{y} = 3_{x}+2_{y} = 4_{x}+1_{y} = 5 $

$ 1_{x}+5_{y} = 2_{x}+4_{y} = 3_{x}+3_{y} = 4_{x}+2_{y} = 5_{x}+1_{y} = 6 $

where, the first diagonal ($n = 1$) is a point, second ($n = 2$) is a line and so on.

So, the pattern would be

$$ \begin{aligned} 1_{x}+n_{y} &= 2_{x}+(n-1)_{y} \\ &= 3_{x}+(n-2)_{y} \\ &= 4_{x}+(n-3)_{y} \\ &=\ldots\\ &= n_{x}+1_{y}\\ & = n+1. \end{aligned} $$

Thus, we can write

$F_{k=1}^{n}~ k_{x}+(n-k+1)_{y} = n+1$.

This means,

when n =1 (first diagonal),  $F_{k=1}^{1}~ k_x + (1-k+1)_y$ gives $1_x + 1_y$,

when n = 2 (second diagonal), $F_{k=1}^{2}~ k_x + (2-k+1)_y$ gives $1_x + 2_y$ and $2_x + 1_y$,

when n = 3 (third diagonal), $F_{k=1}^{3}~ k_x+(3-k+1)_y$ gives $1_x + 3_y$, $2_x + 2_y$ and $3_x + 1_y$ and so on.

This means you can generate the same as given by definition 1.

Definition 2. Let us define a notation named functional notation (i.e. F-notation) and given by $F^{n}_{k=1}$. It states that when the different operation has the same solution then, F-notation is $f(n)$.

Since, $F_{k=1}^{n}~ k_{x}+(n-k+1)_{y} = n+1$ satisfy the definition 2. So, $f(n) = n+1$. Now, it’s very easy to test whether this function gives countably infinite or not, by proving whether it is bijective or not.

Test1.  Let,

$ f(n_{1}) \neq f(n_{2})$

$\Rightarrow (n_{1}+1) \neq (n_{2}+1)$

$\therefore$ $n_{1} \neq n_{2}$.

Hence, the function $f(n)$ is one-to-one.

Test 2. Let,

$m = f(n)= n+1$

$\Rightarrow m = n+1$

$\Rightarrow n= m-1$

Therefore, the inverse function is $f^{-1}(m)=(m-1)$.

Since, $m\geq 2 $ and $ n \geq 1 \mid m\in \mathbb{N}$.

Thus, $f^{-1}(m)=(m-1) \in \mathbb{N}$ i.e. $f^{-1}(m) \geq 1$.

The inverse of the given function $f^{-1}(m)=(m-1) \in \mathbb{N}$ where $f^{-1}(m) \geq 1$ satisfy the domain elements. But as far we know, $f(n)=n+1 \in \mathbb{N}$ as $f(n) \geq 2$. This means the range is equal to the co-domain. Hence, the function is onto.

This means $f(n)$ is bijective.

Finally, we proved our statement using the new notation named F-notation.