Find the number of possible choices for x and y when A=100?

Our problem will goes like this:

Take any number $A \in  \mathbb{N}= {1,2,3,…}$, and then, take $x,y \in \mathbb{N}$, where $x \ne y$ and $ x+y=A $. Find the number of possible choices for $x$ and $latex y$ when $A=100$? Order doesn’t matter, e.g. $x=80$ and $y=20$ is same as $x=20$ and $y=80$.**

To solve this problem first let’s tabulate the natural number and its sum as;

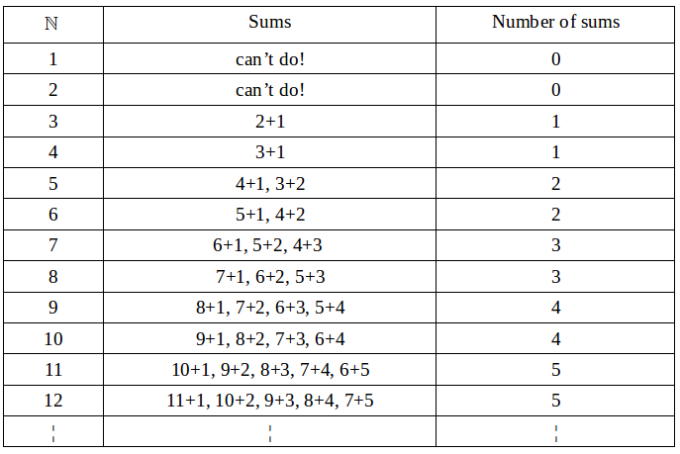
From the above pattern, we can say;

When $A$ is odd, the number of possibilities is $\frac{A-1}{2}$

When $A$ is even, the number of possibilities is $\frac{A-2}{2}$

And hence, the answer is 49 because $A=100$ is even.

If the pattern goes like this then, we can say these formulae are reliable. But if the pattern will break after some natural number then, it won’t work. This means we need a theorem! If anyone could find(or invent) the theorem in regards to this problem. Please do comment below! And also, if you have another method to solve it. Please let me know!

Useful Resources

One can find a wonderful discussion on this problem at Mathematics Stack Exchange: https://goo.gl/uYSzAS .

Still, need to go further

Perhaps one may find this problem very simple. But, I have another similar but extended problem for you. And the problem states like this:

Take any number $A \in  \mathbb{N}= {1,2,3,…}$, and then, take $x, y, z \in \mathbb{N}$ where $x \ne y \ne z$ and $x + y + z= A$. Find the number of possible choices for $x$, $y$ and $z$ when $A = 100$? Note that the order doesn’t matter, e. g. you can do: $x + y + z = A$ or $y + x + z = A$ or $y + z + x = A$ or $z + y + x = A$ or $z + x + y = A$ or $x + z + y = A$. But you cannot do: $x + x + y = A$ or $y + y + x = A$ or $z + z + x = A$ or $z + z + y = A$ or $y + y + z = A$ or $x + x + x = A$ or $y + y + y = A$ or $z + z + z = A$ or soon.

Looks like we also need a general theorem for which we can solve any extended problem. I’m leaving these problems to you on behalf of willing to see its solution. Best of luck!