The premature state of “Topology” and “Graph Theory” nourished by “Seven Bridges of Königsberg Problem”
Many many years ago, there was a problem which created a mind-boggling puzzle to the eminent mathematician named Leonard Euler. But this isn’t the main starting of our story. There was a historical city of Königsberg in Prussia but after World War II, it has been named as Kaliningrad of Russia. Well, I’m not trying to make this story by creating some sad mood but it is the starting point where the problem was created. In that city, there is an island, called the kneiphof; the river (Pregel) which surrounds it is divided into two branches, and these branches are crossed by seven bridges 1. Usually, in the evening time, the people who lived in this city used to gather near to the bridges and entertain themselves. These bridges act as a junction for them. The most entertaining things to them were the seven bridges of that city. Can you guess, how? They were trying to devise a route around the city which would cross each of the seven Königsberg bridges just once and only once. Every time they went to the junction and returned with no answer to that problem. Their ego was hurt badly. Some of them said, there is no any path to cross all bridges at once but they don’t have any concrete ideas to support it. And, many of them believed that the task was impossible. But it was not until the 1730s that the problem was treated from a mathematical point of view and the impossibility of finding such a route was proved 2.
Finally, the problem was given to Euler. As he was trying to give some thoughts in that problem, he saw it has a little link with mathematics and he added, its discovery doesn’t depend on any mathematical principle 3. Again, he was trying to catch which known mathematical principle can be applied. His good luck! He got some clue. The clue was very simple; he stated, this is a geometry problem with no relationship with distances or angles. How can it be a geometry problem which does not have any relationship with distances or angles? As he was trying to understand the problem, he realized there’s the only relationship with bridges, lands, and rivers. He went through the primitive definition of Geometry. Have you ever stated the primitive definition of Geometry? I’ll say, it is a pure branch of mathematics that deals with points, lines, curves, and surfaces. The geometry which we were taught in elementary classes was Geometry of magnitude. He begins to thought bridges as curves or lines and lands as points. And, this is an elementary concept to start with Graph Theory. So, he laid the foundations of Graph Theory. He created the notion that you can start from any of the given bridges. So, he thought that the point where you start acting like the position where you situate. Because you can get the same result from a different position. So he claimed that it should be the problem related to the Geometry of Position. He was aware that, he was dealing with a different kind of geometry where it doesn’t involve measurements and calculations. This kind of geometry was defined by Leibniz and it was in the primitive phase in Euler’s time. Though Leibniz initiated this concept, there wasn’t such a problem that can be solved by this concept. But, Euler found the problem that can be solved by this concept. Today, we call it Topology. This concept suggested that how things connect one to another. It is especially concerned with space and it also studies how properties of a space change and don’t change when space is distorted. In this problem, it doesn’t depend upon either the bridges are long or short, either the position where you start is farther or nearer from the bridges. The points which are concern with the land is actually a position of an experimenter. And the point can be specified in any place within the specific land.
In 1736, Euler published a paper on the solution of the Königsberg bridges problem entitled “Solutio problematis ad geometriam situs pertinentis” which translates into English as “The solution of a problem relating to the geometry of position” 4. His original paper was first published in Commentarii academiae scientiarum Petropolitanae 8, 1741, pp. 128-140 5 and it was the first journal series published by the St. Petersburg Academy 6. In this paper, he proved the problem has no solution. The difficulty was the development of a technique of analysis 7 and to establish the general method to compute not only that problem but others too.
Now, we are dealing with “How Euler solved the Königsberg bridge problem?” and some basics of Graph theory. In Euler’s original paper, He was asked as “Whether anyone could arrange a route in such a way that he would cross each bridge once and only once?” 2. Here, I’ll be discussing only two methods out of three, if you want to read the last method then, you can prefer reference 2 that is mentioned in the section “References”. Also, I’ll be pointing each and every step, analysis, results and conclusions that he made and, make you simple to understand.
Step I: First, we have to give notation to the seven bridges and four land areas. Here, we gave notation to seven bridges as a, b, c, d, e, f, g and four land areas separated by rivers as A, B, C, D and also, replacing the map of the city into simpler diagram showing only river, bridges and lands which is exactly done by Euler.
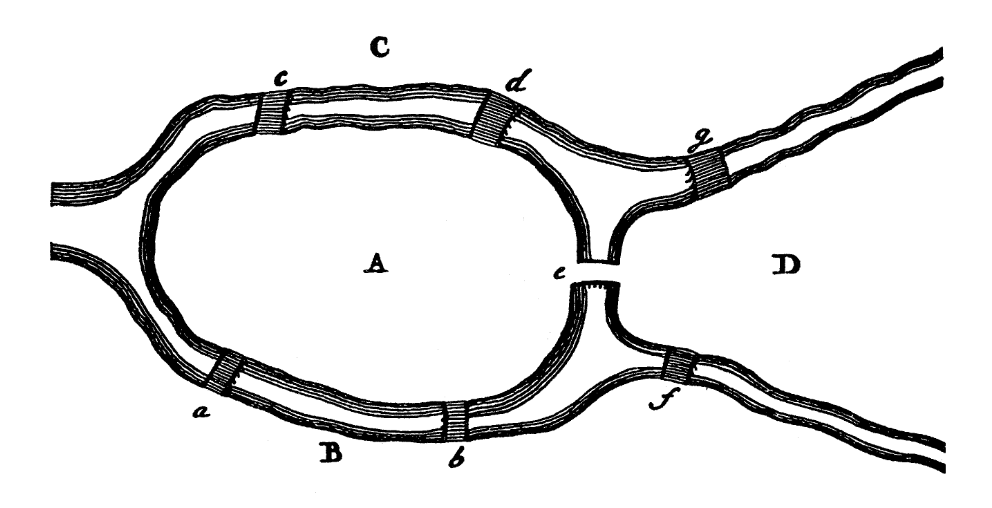
Analysis I: He formulated the general problem as, “Whatever be the arrangement and division of the river into branches, and however many bridges there be, can one find out whether or not it is possible to cross each bridge exactly once?” 2.
Step II: He said, If you go from A to B over bridges a or b, you can write as AB where the first letter says you are leaving from this place and the second letter says you are entering in this place.
Similarly, if you leave B and crosses into D over bridge f then, it can be represented by BD. If you would like to cross AB and BD, it can be represented by the three letters ABD where the middle letter B refers to both the area which is entered in the first crossing and to the one which is left in the second crossing. Then, if you go from D to C over the bridges g, it can be represented by four letters ABDC which says you started from A, crossed to B, went on to D, and finally arrived in C.
Result I: Hence, the crossing of three bridges gave us four letters and, the crossing of four bridges would give five letters. In general, how many bridges the traveler crosses, his journey is denoted by a number of letters one greater than the number of bridges. So, the crossing of seven bridges requires eight letters to represent it.
Conclusion I: Thus, we have to use four letters (i.e. ABCD) in order to represent the possible paths with eight letters.
Analysis II: We are now trying to find such a rule whether or not such an arrangement can exist. Also, we are trying to find what is the number of repetition of a letter A that will appear when we cross an odd number of bridges (i.e. five bridges in our case) from the A or into the land A?
Step III: Let’s make our diagram simple, we will make a river with no branches in it and, which separate the land areas A and B. We put six bridges over the river.
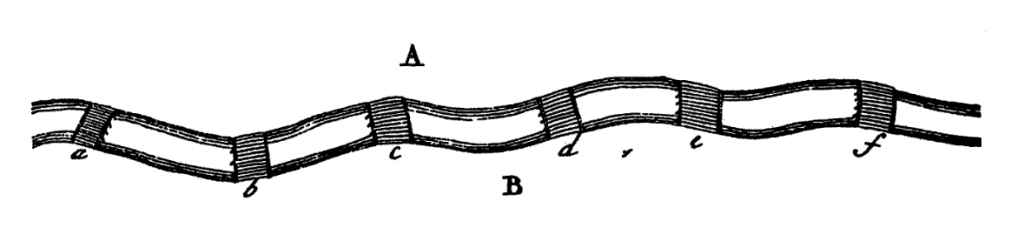
Now, consider bridges only then, we have two cases;
Case I: You must be in A before crossing the bridges a. (i.e. AB) Case II: You have reached A after crossing the bridges a. (i.e. BA)
Hence, A appears exactly once.
Again, consider three bridges a, b and c then, we will found A will occur twice whether you begin from A or not. (i.e. ABAB or BABA) Similarly, consider five bridges a, b, c, d and e then, we will find A will occur thrice whether you begin from A or not. (i.e. ABABAB or BABABA)
Result II: In general, if the number of bridges is odd, first increase it by one and, take half the sum; the quotient represents the number of times the letter A appears. Hence, in the given problem we can say, A occurs thrice, B occurs twice, D and C must occur twice. So, the total number of letters will be nine.
Conclusion II: It says, we have to use four letters (i.e. ABCD) in order to represent the possible paths with nine letters.
Comparison between the Results I and II: From the result I, the possible number of letters should be eight but from the result II, we got nine letters within a similar condition (exactly cross the bridges once and only once). So, we arrived at a contradiction. Hence, the crossing of the seven bridges of Königsberg at once is not possible.
Analysis III: What is the number of repetitions of a letter A that will appear when we cross even the number of bridges from the land A or into the land A?
Step IV: If the number of bridges leading to A is even, then in describing our journey; we have to consider whether or not we start our journey from A. But in the former case, we don’t need to consider this situation. Now, consider two bridges then, we have two cases;
Case I: If we start from A then, the letter A must occur twice. (i.e. ABA)
Case II: If we start from B then, letter A must occur once. (i.e. BAB) Again, consider four bridges then, we have two cases;
Case I: If we start from A then, the letter must occur thrice. (i.e. ABABA)
Case II: If we start from B then, the letter A must occur twice (i.e. BABAB) Similarly, consider six bridges then, we have two cases;
Case I: If we start from A then, the letter A must occur four times (i.e. ABABABA)
Case II: If we start from B then, letter A must occur three times. (i.e. BABABAB)
Result III: In general, if the number of bridges is even, then the number of times the letter A appears will be half of this number if our journey is not started from A, and if our journey does start at A, it will be one greater than half the number of bridges.
Conclusion II: Hence, we can say the number of times the letters appear denoting that area depends on whether the number of bridges leading to each area is even or odd.
In Graph theory, we call bridges as edges, arcs, or lines and areas as vertices, nodes, or points. This will result in a graph! Never confuse with term graph that uses coordinates. This is different, it doesn’t depend upon magnitude. Now we want to define a graph; it is an ordered pair with vertices and edges. It can be denoted as G(V, E). The number of edges connected to a vertex is known as the degree or valency of a vertex. An edge starts from a vertex and end on the same vertex is known as a loop and it can be counted as twice. Also, there is a kind of graph named by several authors as a multigraph. If there are parallel edges and both ends within the same node then, the graph is said to be a multigraph 8. Also, the path that crosses all the given edges at once is said to be an Eulerian path. In the given problem, let’s make the graph of it;
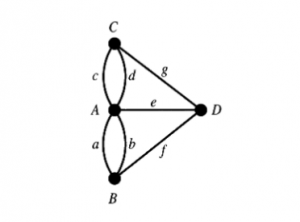
How many nodes, edges, a degree of a vertex and the total number of degrees of vertices are there? Is there is any loop in the graph? From the above comparison between the results I and II, Is there is any Eulerian Path? Is it simply a graph or is it a multigraph? Answer the above question to yourself! It will make you understand some basics of Graph theory. To be noted: The edges shouldn’t intersect each other. If you made it intersected mistakenly then, the point of intersection shouldn’t be counted as a vertex.
Analysis IV: Since we can start our journey from any one land either it may have an odd or even number of bridges leading to it. Euler defines, corresponding to the number of bridges leading to each area, the number of occurrences of the letter denoting that area to be half the number of bridges plus one, if the number of bridges is odd, and if the number of bridges is even, to be half of it 2.
Step V: First, take a total of all the occurrences. Then, if the total of all the occurrences is equal to the number of bridges plus one, the required journey will be possible and will have to start from an area with an odd number of bridges leading to it. However, if the total number of letters is one less than the number of bridges plus one, then our journey is possible starting from an area with an even number of bridges leading to it. Thus, the number of letters will be increased by one. One less is because, we use the result III of not starting from the land, and we don’t know whether we have to start our journey from the land with an even number of bridges leading to it or not start from that land. Increased by one is because we have to use the result III of start from the land with an even number of bridges leading to it.
General Steps:
- For various land areas which are separated from one another by the river, denote it by the letters A, B, C,….
- For a possible path, the total number of letters occurs = 1 + total number of bridges.
- Write the letters A, B, C,… in a column, and right next to each one the number of bridges leading to it.
- Indicate with an asterisk those letters which have an even number of bridges leading to it.
- Next to each even bridges, write half the number and, next to each odd, write half the number increased by one.
- Add all the third column elements.
- If this sum is one less than or equal to, the number of bridges plus one then, we can conclude that the journey is possible. So, there are two cases: Case I: If we get the sum to be one less than the number of bridges plus one then, our journey must begin from one of the areas marked with an asterisk. Case II: If it equals the number of bridges plus one then, our journey must begin from an unmarked one. The final solution to our Königsberg bridge problem: We now are using the above general steps to work out the given problem as: The number of bridges = 7, which yields 8 letters.
| Land | Leading bridges to it | Using Step 5 |
|---|---|---|
| A | 5 | 3 |
| B | 3 | 2 |
| C | 3 | 2 |
| D | 3 | 2 |
Result IV: Since we got more than 8 (i.e. 9). So, such a journey can never be made.
Conclusion IV: Hence, from the comparison between the result I and II, and result IV; we don’t have to be afraid to say, this problem has no solution.
A problem for you:
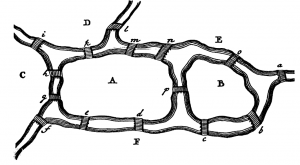
Condition: You can cross each bridge once and only once.
- How many letters that we need to represent our possible path?
- Can we make our journey possible or not?
- If yes then, can you find such a route in which you cross each and every bridge once and only once?
- Can you write all the paths for the possible route?
- Draw a graph of this problem?
- How many nodes, edges, a degree of a vertex and the total number of degrees of vertices are there?
- Is there is any loop in the graph?
- Is there is any Eulerian path?
- Is it simply a graph or is it a multigraph? Apply the general steps in this problem and answer the above questions to yourself, also convince your answer is right and whether you have understood the Euler’s method or not?
For curious people
How many possible ways to cross the bridges at once, if we know the problem has a solution*? (Problem relating to Combinatorics)*
In a nutshell, Euler’s work on this problem showed us some understanding of the primitive phase of Topology and Graph Theory.
References
Barnett, J. H. (n.d.). Early Writings on Graph Theory: Euler Circuits and The Königsberg Bridge Problem. Resources for Teaching Discrete Mathematics Classroom Projects, History Modules, and Articles, 197-208. doi:10.5948/upto9780883859742.026 ↩︎
Biggs, N. L. (1976). Graph theory, 1736-1936: Norman L. Biggs, E. Keith Lloyd Robin J. Wilson. ↩︎ ↩︎ ↩︎ ↩︎
Alexanderson, G. L. (2006). About the cover: Euler and Königsberg’s Bridges: A historical view. Bull. Amer. Math. Soc. Bulletin of the American Mathematical Society, 43(04), 567-574. doi:10.1090/s0273-0979-06-01130-x ↩︎
A history of Topology. (n.d.). Retrieved August 16, 2016, from http://www-gap.dcs.st-and.ac.uk ↩︎
E53 – Solutio problematis ad geometriam situs pertinentis. (n.d.). Retrieved August 19, 2016, from http://eulerarchive.maa.org/pages/E053.html ↩︎
Commentarii. (n.d.). Retrieved August 19, 2016, from http://eulerarchive.maa.org/ ↩︎
Seven Bridges of Königsberg. (2016, July 29). In Wikipedia, The Free Encyclopedia. Retrieved 06:22, August 16, 2016, from https://en.wikipedia.org/ ↩︎
Multigraph. (2016, March 24). In Wikipedia, The Free Encyclopedia. Retrieved 08:29, August 19, 2016, from https://en.wikipedia.org ↩︎
Any feedback?
If you guys have some questions, comments, or suggestions then, please don't hesitate to shot me an email at [firstname][AT]physicslog.com or comment below.
Liked this post?
If you find this post helpful and want to show your appreciation, I would appreciate "a Coffee or Nepali Chi·ya (चिया)". It's a small gesture that can make my day!
Want to share this post?

