A detailed procedure for the synthetic division when the divisor is a second-degree polynomial

You most probably have learned the synthetic division method for the polynomial when divided by $x-a$. But, what if the divisor is a second-degree polynomial? Now, the method you were trained will not work.

In this post, I will try to explain a bit more detail about the method which will work for our proposed problem. Let me start by defining a general expression for the polynomial as $P(x) = a_{0}x^{n} + a_{1}x^{n-1} + a_{2}x^{n-2} + \ldots + a_{n-1}x + a_{n}$. Lets say, our divisor will be $x^{2} + Kx + L$ and reminder be $R$. I must say, when you divide a polynomial of degree $n$ by another polynomial with degree $m$ then, the quotient will have a degree of $n-m$. This means, in our case, we have a divisor with degree $2$. So, our quotient will look like this $Q(x) = b_{0}x^{n-2} + b_{1}x^{n-3} + \ldots + b_{n-3}x + b_{n-2}$.

If we use the Euclidean division algorithm which says “if you divide integers then, it produces a quotient and a remainder smaller than the divisor”. For our case,

$P(x) = Q(x)(x^{2} + Kx + L) + R$

$ = (x^{2} + Kx + L)(b_{0}x^{n-2} + b_{1}x^{n-3} + \ldots + b_{n-3}x + b_{n-2})$

$ = (x^{2} + Kx + L)(b_{0}x^{n-2}) + (x^{2} + Kx + L)(b_{1}x^{n-3}) + (x^{2} + Kx + L)(b_{2}x^{n-4}) +\ldots + (x^{2} + Kx + L)(b_{n-1}x) + (x^{2} + Kx + L)(b_{n-2}) + R$

$= (b_{0}x^{n} + Kb_{0}x^{n-1} + Lb_{0}x^{n-2}) + (b_{1}x^{n-1} + Kb_{1}x^{n-2} + Lb_{1}x^{n-3}) + (b_{2}x^{n-2} + Kb_{2}x^{n-3} + Lb_{2}x^{n-4}) + \ldots + (b_{n-1}x^{3} + Kb_{n-1}x^{2} + Lb_{n-1}x) + (b_{n-2}x^{2} + Kb_{n-2}x + Lb_{n-2}) + R$.

Now, we collect the terms so that we can form a polynomial. i.e.

$P(x) = b_{0}x^{n} + (Kb_{0} + b_{1})x^{n-1} + (b_{2} + Kb_{1} + Lb_{0})x^{n-2} + (b_{3} + Kb_{2} + Lb_{1})x^{n-3} + \ldots + (b_{n-2} + Kb_{n-1} + Lb_{n})x^{2} + (Kb_{n-2} + Lb_{n-1})x + (Lb_{n-2} + R)$

It looks like we can compare with the polynomial $P(x)$ as

$a_{0} = b_{0} \implies b_{0} = a_{0},$

$a_{1} = b_{1} + Kb_{0} \implies b_{1} = a_{1} - Kb_{0},$

$a_{2} = b_{2} + Kb_{1} + Lb_{0} \implies b_{2} = a_{2} - Kb_{1} - Lb_{0},$

$a_{3} = b_{3} + Kb_{2} + Lb_{1} \implies b_{3} = a_{3} - Kb_{2} - Lb_{1},$

$\ldots \implies \ldots,$

$a_{n-2} = b_{n-2} + Kb_{n-1} + Lb_{n} \implies b_{n-2} = a_{n-2} - Kb_{n-1} - Lb_{n},$

$a_{n-1} = Kb_{n-2} + Lb_{n-1} \implies a_{n-1} = Kb_{n-2} + Lb_{n-1},$

and $a_{n} = Lb_{n-2} + R \implies R = a_{n} - Lb_{n-2}$.

If we make supposition $A = -K$ and $B = -L$ then, above compare becomes

$b_{0} = a_{0},$

$b_{1} = a_{1} + Ab_{0},$

$b_{2} = a_{2} + Ab_{1} + Bb_{0},$

$b_{3} = a_{3} + Ab_{2} + Bb_{1},$

$\ldots,$

$b_{n-2} = a_{n-2} + Ab_{n-1} + Bb_{n},$

$0 = a_{n-1} + Ab_{n-2} + Bb_{n-1},$

and $R = a_{n}  Bb_{n-2}$.

At last, you will know why I made this supposition!

Have you notice there is no $b_{n-3}$? This means $b_{n-3} = 0$. This is because the degree of quotient is $n-2$. So we can say,  $b_{n-3}$ must equal to $a_{n-1} + Ab_{n-2} + Bb_{n-1}$. i.e.

$b_{n-3} = a_{n-1} + Ab_{n-2} + Bb_{n-1} = 0$.

In most of the case, a remainder is simply a number (i.e. $R(x) = R$) but, if the remainder is a polynomial then, we need to write  $R(x) = b_{n-3}x + R$. This happens if $b_{n-3} \neq 0$. I would be very happy if you could find it by yourself why we can write $R(x) = b_{n-3}x + R$.

Now, we have all the ingredients to make a method that works for us. Thus, the method looks like this:

. The red line shows $b_{0} = a_{0}$. This is our initial visualization.

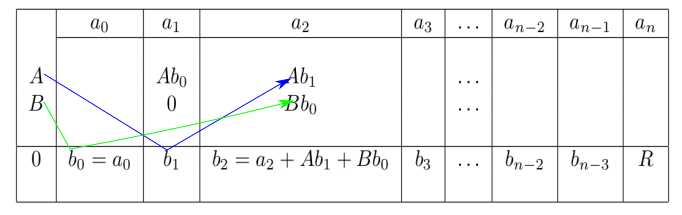
In this figure, the blue line shows $A$ is multiplied by $b_{1}$ and the green line shows $B$ is multiplied by $b_{0}$. This means, $A$ always multiply one term further than $B$. All the elements of the fourth column are then added and equal to $b_{2}$.

Similarly,

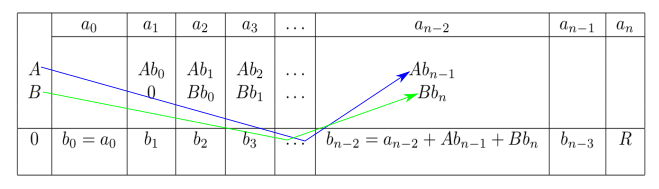
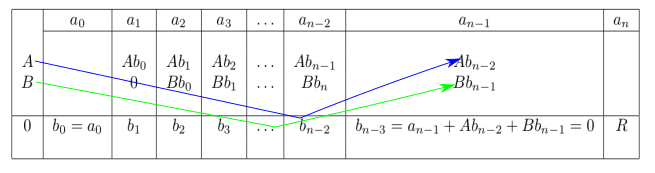
. The last figure is our final visual method for the synthetic division when the divisor is second-degree polynomial.

Before finishing this post, isn’t it great if we can implement this visual method in any one related example? So, our example goes like this: “Find the quotient and remainder when $3x^{6} - 4x^{5} - 5x^{4} + 34x^{3} - 31x^{2} + 32x + 9$ is divided by $x^{2} - 3x + 4$ ?”

Our solution starts as $A = -K = -(-3) = 3$ and $B = -L = -4$. Now, by using our visual method, we can have

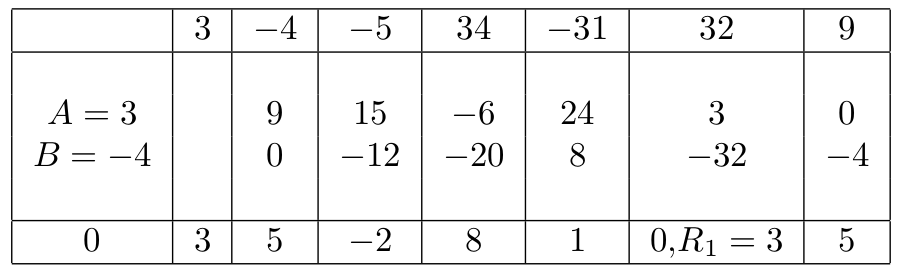
. Hence, the quotient is $3x^{4} + 5x^{3} - 2x^{2} + 8x + 1$. Since the sum of the second last column is not equal to zero so, the remainder becomes $3x + 5$. I must say, when you multiply $(A = 3)$ with second last column’s last row then, you should multiply it with $0$, not $3$.

Quick Question for You

Lastly, if you could write a program (in any programming language except maths 😃) to implement this method then, please feel free to share it with all of us via comment.